Protínají se rovnoběžky v nekonečnu? Aplikace na trojúhelník

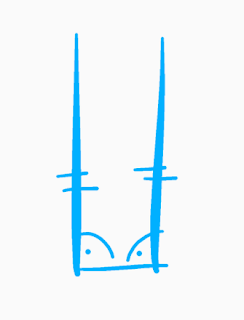
V hospodě jsme se dostali k zajímavému problému. Tím byla definice trojúhelníku za pomocí dvou rovnoběžek tak, jak je to znázorněno na náčrtku.

Autor věty říká, že jde o trojúhelník, protože se rovnoběžky protínají v nekonečnu.

Všichni intuitivně cítíme, že tato úvaha není správná, nicméně není úplně mylná, pojďme ale matematicky ukázat v čem je problém. Sázka byla o půl litr točené Kofoly a to už stojí za pár hodin pročítání matematických skript. 

Moje prvotní myšlenka byla, že to ztroskotá na vágním zadání, přičemž jsem byl ihned spolusedícími upozorněn, že nemám používat divná slova, kterým nerozumí. (což je samo o sobě docela složitý problém).

Vycházejme z toho, že se celý příklad odehrává "za normálních podmínek". Elementární definice rovnoběžek vychází z jejich podstaty v Eukleidově prostoru (to je ten "náš normální", pak je i spousta dalších).

Axiom rovnoběžnosti z pátého Eukleidova postulátu: Každým bodem B, který neleží na přímce p, lze vést právě jednu přímku p′, která neprotíná p. 

Intuitivně z toho vyplývá, že rovnoběžky se nikde neprotínají. Jak vidíte Eukleides neznal pojem nekonečno, jeho geometrické axiomy jsou staré cca 2000 let, protože nekonečno jako pojem se podařilo zkrotit teprve odhadem 300 let zpátky. Přesto se občas vyskytuje tvrzení, že se rovnoběžky protínají v nekonečnu. (respektive se mi nepodařilo najít žádný věděcký zdroj informací, který by tuto myšlenku podpořil)

Nicméně připusťme pro zbytek článku, že se rovnoběžky skutečně protínají v nekonečnu, na řešení to nebude mít vliv. Tím by došlo k naplnění představy o tom, že vznikne trojúhelník.

Každopádně je hledání řešení přes vyvracení axiomů příliš složitý akademicko-matematický problém. Dostanete se tím do elementárních termínů geometrie a do jiných než euklidovských prostorů.

Co mě v zápětí napadlo (při připuštění protnutí), je zaměřit se na druhý pojem a tím je trojúhelník:

Základní vlastností trojúhelníka v euklidovském prostoru je jeho určení třemi body, neležícími v jedné přímce a skutečnost, že součet velikostí jeho vnitřních úhlů je roven 180°.

Pokud tedy dvě přímky svírají svírají ůhly 90° ke své kolmici, pak jejich součtem vyjde přesně číslo 180. Protnutím polopřímek v nekonečnu by vznikl sice třetí bod neležící na jedné přímce, ale také ještě nekonečně malý úhel, jehož přičtením ke 180° by byl porušen součet vnitřních úhlů a výsledný útvar by nebyl trojúhelníkem. 

Tím jsem našel spor v původním tvrzení a Kofola by měla připadnout mi. À propos neuvažujte o nekonečnu jako o číslu, tedy ani jako o bodu, který je možné geometricky využít. 

Jak jsem naznačil, tak pravdivost celá úlohy byla postavena na připuštění jevu o protnutí a dost nepřesném zadání. Při dalším rozboru totiž dojdeme ke zjištění, že v neeukleidovské geometrii se součet úhlů v trojúhelníku liší od 180°. 

Pro řešení by pomohlo přenesení náčrtku do eliptické  geometrie. Zde ovšem vzniká problém s tím, že v tomto prostoru neexistují rovnoběžky, protože se dvě přímky z principu vždy protnou. Příbuzným problémem je Saccheriho čtyřúhelník.

Nicméně to nebylo v zadání explicitně (pardon výslovně) uvedeno a tak to nelze předpokládat. Navíc obrázek je zakreslen značením platným v Eukleidově prostoru. Zkrátka Kofola je moje.

Jisté zjednodušení pro pochopení problematiky vede obecně k možnosti napadnutelnosti textu pro jeho nedokonalost. V matematice je totiž nutné být přesný a používat specifikované termíny definovaným způsobem (vidíte, jak to dopadá), což je také důvod, proč jsou vysoce postavení matematici a) tak nesrozumitelní b) tak příšerně nudní pro nezaujaté posluchače.

Tímto článkem jsem chtěl nějak pochopitelně objasnit uvedený hospodský problém. Respektive tvrzení, kterým jeho autor vyvedl z míry učitelku matematiky na střední škole. Předpokládám, že je v něm spousta více či méně podstatných nepřesností (resp. že původní tvrzení je příliš velká blbost). Budu rád, pokud mi o nich dáte vědět v komentářích níže. 

Pokud máte i nadále pocit, že matematika je děsně nudná záležitost, tak vám doporučuji si přečíst třeba problém Rusellova paradoxu, paradox lháře (či nějaký jiný).  I když to úplně nesouvisí s problematikou geometrických prostorů.

Pokud navíc patříte k těm, co tvrdí, že se dá všechno snadno a rychle vyřešit (ať už jde o politiku, sociální otázky nebo cokoliv jiného), pak snadno přelouskáte i nějaké dosud nevyřešené matematické problémy.

Zdroje:

• odkazy použité v textu
• Háňa Bendová - Neeukleidovská geometrie 
• Kristýna Křížová - Neeuklidovská geometrie
• Wikipedie - heslo euklidovský prostor
• Wikipedie - Neeukleidovská geometrie
• Wikipedie - heslo trojúhelník

Tento příspěvek jsem také vyvěsil na své sociální sítě, kde se mi k němu ozvali mí kamarádi, kteří se matematikou zabývají na profesionálnější úrovni než já. Dovolil jsem si svůj původní článek podle jejich poznatků lehce modifikovat, ale zároveň chci předat jejich myšlenky dalším čtenářům:

Kamil Keprt (OSU): Tvrzení, že když přičteš nekonečně malý úhel ke 180 dostaneš více a proto to není trojúhelník se mi zdá velmi pochybné. Spíše bych řekl že v EP prostě žádné body v nekonečnu dělat nemůžeš, takže vše s čím skončíš jsou 2 body a ne 3... Do celé té Euklidovské geometrie bych nekonečno neplantal, ta na to prostě není stavěná. Jak se tam zaplantá nekonečno, tak jsou z toho reálné projektivní prostory a různé nepředstavitelné "hnusy". Za mě: Jestli dvě rovnoběžky určují trojúhelník? V EP ne, v jiných geometriích ano... Každopádně zajímavá úvaha...

Podíval bych se na to z topologického hlediska (tomu bych mohl rozumět více než geometrii), tak Eukleidovská rovina jak ji známe ze střední má svoji metriku (můžeš určit vzdálenosti libovolných dvou bodů), metrika indukuje topologii (ta říká co je otevřená množina a co ne), která je naprosto schodná s přirozenou topologií (otevřené množiny jsou prostě řečeno ty s čárkovaným okrajem, když je kreslíš) a R^2 je triviální 2 dimenzionální varieta nad R, a teď k té myšlence po té spoustě chytře vypadajících keců: 

V každém bodě je okolí, které je "homeomorfní" (spojitě můžeš přecházet tam a zpět) s tou vaší A4 papírem řekněme - a na tom papíře můžeš určit souřadnicový systém a "blabla" a můžeš si tam nakreslit různé body a měřit mezi nimi vzdálenosti atd... ten svůj papír zároveň můžeš "změnou měřítka" zvětšovat jak je libo, ale nikdy nenakreslíš bod nebo cokoliv na přesný okraj toho papíru, ten okraj je "čárkovaný", tomu papíru nepatří, můžeš se k němu jen libovolně blízko přiblížit, ale pořád to nebude na tom okraji, na tom okraji by se nacházelo to "nekonečno", ale v této struktuře to prostě nejde...

Dominik Koutný (UPOL): V euklidovské, obecně afinní, rovině se dvě rovnoběžky z definice neprotnou. Jde o to, že se dá nadefinovat něco jako "přímka v nekonečnu", a pak se rovnoběžky protnou, ale už pracuješ s projekcemi a projektivními prostory.  Proto se asi říká, že se rovnoběžky v nekonečnu protnou.

K tomu, jak říkáš že by to už nebyl trojúhelník, tam bych viděl problém v tom, že považuješ nekonečno za pevný bod, pak by součet skutečně nebyl 180°, ale jiný. Nekonečno je ale abstraktní skruktura, takže bys přičítal nulu, jelikož platí, že pro tvůj pevně daný úhel bys vždycky dokázal najít menší, takže by ti to šlo k nule. Existují však transformace, které ti nekonečno přitáhnou do bodu a pak je s ním možné pracovat jako s bodem, ale není to součástí EP. Ve fyzice jsou takové transformace běžné, např. funkce Arkus tangens ti přitáhne nekonečno do PI/2, ale to je jenom nástin, jak to může fungovat. Všechno je taky otázka definice. Říkám jenom, co jsem pochytil sem tam na hodinách, můžu se mýlit.

motikona smile.

Zdá se, že celý problém není vůbec triviální. Jako vždy pomůže, pokud se už na začátku pokusíte problém řešit intuitivně a až poté si jej začít ověřovat pomocí pouček.

Jestli chcete v tématu pokračovat, následující článek renomovaného autora jakoby v nakousnutém tématu pokračoval mnohem dále...